How a five-line stave does so much
8th September, 2018
It seems to be a cross-cultural universal that musical pitches are conveyed using the metaphor of height. Across languages and cultures, sounds are described as being “high” or “low”. This metaphor is carried over to Western music notation in the vertical placement of note heads on a grid of horizontal lines called a stave (or staff in the US).
On reflection, it is interesting that the notation evolved into a stave of just five lines. A mixed choir has a comfortable range of around 40 semitones and a modern piano has 88 keys and yet a five-line stave is sufficient to convey any one of those possible pitches.
How this is done in common Western notation says a lot about how Western music in the Common Practice Period (17th to 19th century) works but it also more says a lot about how encoding for communication works in general. The mechanisms discussed in this post are a basic part of music theory but I think it’s at least interesting to discuss them in the specific context of how a restricted encoding scheme (the five-line stave) is able to convey such a wide range of pitches efficiently.
There is one “quick trick” used and then two “big ideas”. Each of the big ideas consists of a simplifying assumption and a mechanism or two for dealing with exceptions.
The quick trick is simple: distinguish both lines and spaces and allow any given note head to be either on a line or in a space. This effectively doubles the number of positions that can be expressed on a five-line stave (nine if you just use the spaces between the lines and 11 if you allow for the space above the top line and below the bottom line, which we’ll assume from now on). It is easy enough when reading a score to distinguish whether a note head is on a line or space (at least in printed notation—some composer manuscripts can be a little tougher!).
But even 11 is shy of an octave (which has 12 semitones) and a long way from 40 much less 88!
And here’s where we come to the two “big ideas” which both make use of an important pattern in encoding for communication:
Make the common cases really simple while providing a (more complex) way of handling the other cases.
The first “big idea” involves the simplifying assumption that the notes are just the diatonic notes of the scale. In other words, instead of giving all 12 notes in the octave their own position, just give the seven diatonic notes their own position. In many works, only diatonic notes appear (or at least make up the vast majority) and so this is a very efficient trick. It means that our five-line stave can now span one-and-a-half octaves: an 18 semitone range (albeit only distinguishing 11 of those 18).
Of course, we need a way of indicating what key we’re in because this determines which notes are the diatonic ones. This is the role of the key signature. The key signature tells us, either globally or for a particular section of a work, which seven of the 12 possible notes are diatonic. We’ll have a lot more to say in future posts about how all this works (why seven? why 12? what constraints exist and why?) but the key here (pun intended) is that we have a way of making a simplifying assumption in our encoding (only diatonic notes get their own position) and a way of conveying what assumption we’ve made (with a key signature). So, for example, here is a D major scale-and-a-half where the F and C are sharpened as indicated by the key signature:

We still need a way of indicating exceptions. We want to make the common case simple to encode, but we don’t want to exclude communicating the rarer cases all together. Our mechanism for exceptions here is the accidental. We can indicate on a per-note basis (or perhaps per-measure, depending on the notation convention) that the pitch is not diatonic but is a semitone above or below a particular diatonic. For example, here are all 18 chromatic notes in our octave-and-a-half:

The accidental used depends not only on whether we want a semitone higher or lower but whether the diatonic note is itself natural, sharp, or flat:
| diatonic note | accidental for semitone higher | accidental for semitone lower |
|---|---|---|
| natural | sharp | flat |
| sharp | double sharp | natural |
| flat | natural | double flat |
Our second “big idea” involves the simplifying assumption that large jumps are very rare and, for the most part, a given instrument or voice (or individual hand on the piano) will stay within a particular range for large parts of the piece. This is, in fact, why only five lines are sufficient: the octave-and-a-half range it allows covers the vast majority of cases. In particular, it’s quite an appropriate range for vocal parts. The problem is: which particular octave-and-a-half “window” do you want to assume at any given point? And how do you indicate your assumption?
Well, just as the key signature is used to signal the assumption about key (and hence what the diatonic notes are), the clef signals the assumption about the particular range of notes that we most efficiently want to convey.
Imagine if we were writing a piece for mixed choir that ranged from F near the bottom of a bass singer’s range to the G near the top of a soprano singer’s range. A single stave to convey that range of 39 notes would require an 11-line stave!
Here we hit a readability problem. With 11-lines it’s much harder to see at a glance where a particular note is located. Five lines seems quite optimal because it’s very quick to see whether a line is at the top, between the top and middle, the middle, between the middle and bottom, or at the bottom.
Fortunately, different voices (and corresponding instruments) will (and this is our simplifying assumption) tend to stay within a subset of the 11-line stave. A bass part might generally only need the bottom five lines, an alto part the middle five lines, the treble part the top five lines and so on. What we need is a way of indicating where a given five-line stave fits in a larger pitch range.
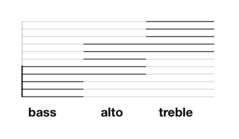
It so happens that the line in the middle of our 11-line stave above is middle-C. This gives us an origin of sorts to locate ourselves. Unfortunately, the bottom five lines don’t include the middle-C line and nor do the top five lines so we need some additional reference pitches to locate our stave with. We’ll choose the F below middle-C and the G above middle-C.
Any five-line subset of our 11-line stave will include at least one of: the middle-C line, the F below middle-C line, and the G above middle-C line.
So it’s enough to identify, in any five-line subset, one of these three lines.
And that’s exactly what the clef is doing. The “F” clef indicates where the F below middle C is, the “C” clef where the middle C is and the “G” clef where the G above middle C is:
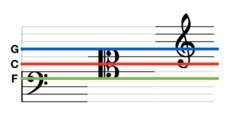
The most common way to use the “F” clef is to pick the five lines such that the second line (from the top) is F below middle-C and, in this case, it’s commonly known as the bass clef. Other line selections with an “F” clef are very rare. The most common way to use the “G” clef is to pick the five lines such that the fourth line is G above middle-C and, in this case it’s commonly known as the treble clef.
The selection of lines around the “C” clef can vary. The most common choice is for middle-C to be the middle line in which case it’s commonly known as the alto clef. This is found in viola parts. The choice of lines such that middle-C is on the second line is also found, for example, in some ‘cello parts. In this case the “C” clef is called the tenor clef. Much rarer, but found in some older vocal scores is the “C” clef used as a soprano clef, mezzo-soprano clef, or baritone clef. Each of these names is indicative of the range the clef is suited for.

In the above, middle-C is shown with a red line in each case.
Much like we can change the key signature at any point, we can change the clef, but there are two other mechanisms for handling exceptions. One is ledger lines. In small doses, and if only a few are used, these can be very readable and an efficient way of extending the range of a stave by half-an-octave or so in either direction.

The other mechanism is the ottava sign to indicate a sequence of notes are to be played an octave higher or lower than notated.

The ottava sign can also be combined with a clef where the octave shift extends for the duration of the clef. This is common, for example, in vocal music written for tenors. Some orchestral instruments do this by convention, even if not marked explicitly: the piccolo is always written an octave lower than it sounds and the double bass an octave higher that it sounds. Although outside the scope of this blog post, there are also numerous transposing instruments for which this is done at intervals other than an octave.
All of these mechanisms, when combined, allow us to handle the range of mixed choirs, pianos and more, within the very easy-to-read five-line stave.
Beyond the “use lines and spaces” trick, we can summarise these techniques in the following table:
| simplifying assumption | indication of assumption | mechanism for exceptions |
|---|---|---|
| only diatonic notes | key signature | accidentals |
| octave-and-a-half range | clef | ledger lines, ottava sign |
The communication of pitch on a stave is thus made more efficient by making simplifying assumptions while still allowing exceptions to be expressed. The particular simplifications used are indicative of much of Western music in the Common Practice Period.
Many thanks to A. E. Maresia for feedback on an earlier draft of this post.